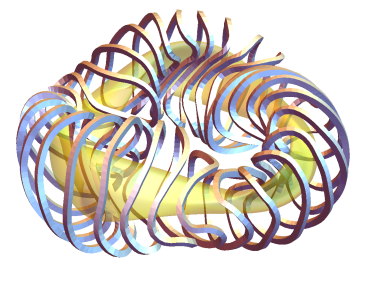
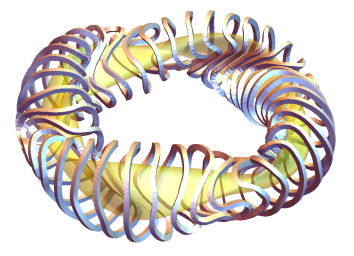
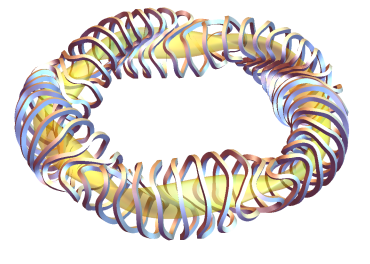
Stellarator Model

The code has the ability to perform calculations based on the physics and engineering of a stellarator, which, although being a toroidal device, is radically different in a number of ways from a tokamak.

The model is largely based on W7-X and the HELIAS 5-B stellarator power plant design¹ (Figure 1) and related modelling that has been performed by IPP Greifswald^{2 3 4 5}

Figure 1: Fusion power core of the HELIAS 5-B conceptual power plant design¹

To activate the stellarator coding, it is necessary to create a file deivce.dat, containing the single character 1 in the first row, in the working directory. This has the effect of setting the internally-used switch istell = 1. If the file is absent, or its first character is set to something other than 1, the stellarator model is not used, and istell is set to 0.

Stellarators in PROCESS

PROCESS can model any module stellarator reactor when provided with a dedicated input file. The procedure use is based on the prescription described in ⁶, using a set of pre-calculated parameters which needs to be provided by a file with the name stella_conf.json which can be calculated by the pre-sPROCESS code ⁶. This functionionality is enabled by istell=6, and PROCESS will then expect the configuration file stella_conf.json in the same directory as the input file. Using istell=6 is the advised way to use the stellarator version of PROCESS as no hardcoded stellarator-parameters are being used in this case.

Nevertheless, there are four types of stellarators which can be used without providding the configuration file, a HELIAS type stellarator with 3, 4 or 5 field periods as described in the collected paper ¹³, and a W7-X like stellarator.

Figure 2: Different HELIAS stellarator types, implemented as istell=1,2,3¹

The user can switch between these models by using the switch variable istell:

• istell=1: Helias-5
• istell=2: Helias-4
• istell=3: Helias-3
• istell=4: W7-X
• istell=5: A W7-X variation with 30 coils
• istell-6: Use the stella_conf.json file.

The stellarator version of PROCESS assumes the coil-set itself to be fixed in shape and can only scale the overall size of the machine in major radius rmajor. There is no capability in PROCESS to seperately scale the minor coil radius -- in other words: the coil aspect ratio is fixed. Also the number of coils is considered fixed and is given by the configuration.

Input File Specifications

The following consistency equations should be used without modifications:

icc = 2 * Global Power balance
icc = 82 * Toroidal build at critical location (inequality)
icc = 83 * Radial build at critical location (inequality)

A reasonable start for a stellarator run is the following set of constraints:

icc = 2 * Global Power balance (core)

* Inequalities
icc = 8  * Neutron Wall load limit
icc = 17 * Global Power balance overall (needed to limit radiation)
icc = 18 * Divertor power limt
icc = 24 * Plasma Beta limit
icc = 32 * Maximal Coil Stress on Ground insulation (approx.)
icc = 34 * Dumping voltage during Coil Quench
icc = 35 * Temperature rise during Coil Quench
icc = 65 * Stress on VV rise during Coil Quench
icc = 82 * Toroidal build at critical location
icc = 83 * Radial build at critical location
icc = 91 * ECRH ignitability (checks critical density at ignition point)

A reasonable start for iteration variables (next to the required f-values) are:

ixc = 2 * Toroidal Magnetic field strength
ixc = 3 * Major Radius of the machine
ixc = 4 * Electron Temperature
ixc = 6 * Electron Density
ixc = 10 * "ISS04 Renormalization Factor" (can also be fixed)
ixc = 50 * Coil current density, aka winding pack thickness (required!) 
ixc = 59 * Winding Pack copper fraction
ixc = 56 * Exponential Quench Dumping Time
ixc = 109 * Thermal alpha particle pressure (iterated to consistency, use together with `taulimit`)
ixc = 169 * Achievable Temperature of the ECRH at the ignition point

Code specifics

The stellarator model is largely contained within source file stellarator.f90.

The model call is in the following order

1. Stellarator New Configuration setup (stnewconfig)
2. Stellarator Geometry (stgeom)
3. Stellarator Physics Loop Routine (containing steps requiring to evalute the physics model at different operation points) (stopt)
4. Stellarator Physics (stphys)
5. Stellarator radial and toroidal build (stbild)
6. Stellarator Structure Mass (ststrc)
7. Stellarator first wall, blanket and shield module (stfwbs)

8. Stellarator Divertor (stdiv)

9. TF coil power consumption

10. Heat Transport Model (First part)
11. Power Plant Buildings
12. Vacuum Model
13. AC power requirements model
14. Heat Transport Model (Second part)
15. Availablity
16. Costs

Calls 1-8 are stellarator specfic, although use certain overlap with the tokamak modules as will be addressed more in detail below. Calls 9-16 use the tokamak models and assume applicability also to stellarators. In these calls, there are if (istell == 0) then calls in these models implemented if certain steps are not applicable.

Stellarator physics

Much of the physics is identical to that for tokamaks, including the plasma composition and the fusion power calculations. However, some physics topis do differ between stellarators and tokamaks, as follows.

Plasma geometry

The plasma geometry model uses precalculated effective values from Fourier coefficients to represent the complex 3-D plasma shape typical of stellarators. A VMEC⁵ calculation (or other equilibrium code that can provide the Fourier coefficients of the LCFS) can be used to obtain the respective effective parameters. The overall size of the plasma is scaled correctly for the required (mean) major and minor radii for the machine being modelled⁶.

Absence of plasma current

Stellarators try to achieve zero plasma current in order to allow safe divertor operation, so no current scalings are required.

Beta limit

The stellarator version calculates the plasma beta based on the input parameter and it is thus not necessary to Differently to the tokamak version, The beta limit is assumed to be 5%, based on 3-D MHD calculations⁷. To apply the beta limit, constraint equation no. 24 should be turned on with iteration variable no. 36 (fbetatry).

Density limit

The density limit relevant to certain stellarators experiments has been proposed to be⁸

$n_{max} = 0.25(PB_0/R_0a^2_p)^{1/2}$

where $n$ is the line-averaged electron density in units of $10^{20} m^{-3}$, $p$ is the absorbed heating power (MW), $B_0$ is the on-axis field (t), $R_0$ is the major radius (m), and $a_p$ is the plasma minor radius (m). To enforce the Sudo density limit, turn on constraint equation no. 5 with iteration variable no. 9 (fdene).

Note that the Sudo limit is a radiation based density limit and it is unclear how well this limit extrapolates to reactor parameters, especially as no impurity dependence e.g. is present in the Sudo model. PROCESS features an impurity dependent radiation module already which can be used with icc=17 and by setting the fimp vector. For certain regimes, this model is able to reassemble a Sudo-like scaling behaviour in the maximal achievable density, see also the density limit chapter in ¹⁵.

In addition to the sudo limit the density in a stellarator is bound by the ECRH heating which requires density values below the critical density. The constraint equation icc=91 together with ixc = 169 enforces that the found design point can in principle be achieved with ECRH O1 heating (it checks if the most performant O1 ECRH heatable design point is ignited).

$\tau_E$ scaling laws

Five confinement time scaling laws relevant to stellarators are present within PROCESS. The value of switch isc` determines which of these in the plasma energy balance calculation.

$\tau_E$ (Large Helical Device⁸: isc=21) = $0.17 \, R^{0.75}_0 \, a^2_p \, \bar{n}^{0.69}_{20} \, B^{0.84}_0 \, P^{-0.58}$
$\tau_E$ (Gyro-reduced Bohm⁹: isc=22) = $0.25 \, R^{0.6}_0 \, a^{2.4}_p \, \bar{n}^{0.6}_{20} \, B^{0.8}_0 \, P^{-0.6}$
$\tau_E$ (Lackner-Gottardi¹⁰: isc=23) = $0.17 \, R_0 \, a^2_p \, \bar{n}^{0.6}_{20} \, B^{0.8}_0 \, P^{-0.6} \, \iota^{0.4}$
$\tau_E$ (ISS95¹¹: isc=37) = $0.079 \, R^{0.65}_0 \, a^{2.21}_p \, \bar{n}^{0.51}_{20} \, B^{0.83}_0 \, P^{-0.59} \, \bar{\iota}^{0.4}$
$\tau_E$ (ISS04¹²: isc=38) = $0.134 \, R^{0.64}_0 \, a^{2.28}_p \, \bar{n}^{0.54}_{20} \, B^{0.84}_0 \, P^{-0.61} \, \bar{\iota}^{0.41}$

Here $\bar{\iota}$ is the rotational transform, which is equivalent to the reciprocal of the tokamak safety factor $q$.

Gradient informed neoclassical transport checks

As no 1D solver options are available for stellarators yet, PROCESS prints several neoclassics parameters as obtained from the 1/$\nu$ regime. The two most important parameters are q_PROCESS and total_q_neo_e. q_PROCESS is the heat flux that PROCESS obtaines from the 0D confinement time scalings. total_q_neo_e is the estimated total neoclassical flux as obtained from the 1/$\nu$ electron transport regime, multiplied by a factor of 4 (2 for the ion contribution and another factor of 2 for the radial electrical field influence). The user should check if q_PROCESS>total_q_neo_e. If not, the design point is likely not feasible.

PROCESS inherits a full neoclassics module with is in principle capable of calculating the radial electrical field and the actual neoclassical fluxes based on mono-energetic transport coefficients with can be passed via the stella_conf.json file, the functionality is already implemented (but not yet accessible for the user yet as no viable pre-processing routines are implemented yet).

Heating power options

Stellarators require no curren drive, although provision for auxiliary heating does need to be present. The method by which auxiliary heating power is supplied is determined by the switch isthtr:

isthtr = 1 : electron cyclotron resonance heating

isthtr = 2 : lower hybrid heating

isthtr = 3 : neutral beam injection

The value of variable pheat determines the actual amount of auxiliary heating power (in Watts) to be applied to the plasma. This variable may be used as an iteration variable (no. 11). Switch ignite may be used if necessary.

Divertor

Although the divertor has the same function in both stellarators and tokamaks, the envisaged concepts differ quite substantially. This is not only related to the different geometry and symmetries but also specifically to the magnet configuration. While the inherent axisymmetry of a tokamak allows for poloidally-continuous single of double divertor configurations, the periodicity of helical advanced stellarators leads to multiple X-points with a corresponding chain of magnetic islands. This island structure may be exploited by carefully placing divertor plates along the stochastic field lines, naturally leading to a discontinuous divertor, with the individual plates being placed in a complex 3-D geometry; see Figure 2.

Figure 3: A five-period HELIAS plasma (specifically W7-X) with island divertor plates shown in red

Rather than trying to describe the complex physics with a two-point scrape-off layer model as is used for tokamaks, the stellarator divertor model³ is based on fundamental principles which relate the power crossing the separatrix with an effective wetted area on the divertor plates allowing the code to estimate the heat load delivered to the divertor. A basic island divertor model is used which assumes diffusive cross-field transport and high radiation at the X-point.

The radiated power fraction in the scrape-off layer is given by the input parameter f_rad. This is in contrast to the method used for tokamaks, in which the radiated power fraction is a calculated quantity.

A number of other input parameters may be used to modify the divertor model; see the variable descriptor file for more details.

Stellarator Technological entities

Stellarator coils

There are a large number of possible stellarator configurations. As stated earlier, PROCESS has the capabilities to model very generic modular stellarator coil sets, based on coil filaments and the plasma shape for geometrical distances. The relevant parameters for PROCESS' scaling laws enter the systems code model via a configuration dependent file called stella_conf.json which needs to be located in the same directory as the input file. This file needs to be prepared by hand or can be written automatically by the pre-sPROCESS ing code.

Alternatively istell = 1,2,3,4,5 allow for pre-selected stellarator machines.

Figure 3: Differences of the stellarator coil cross section in PROCESS compared to the tokamak description. Note the identical thkcas around the cable area.

The stellarator coil model⁶ uses scaling aspects based on a reference calculation of the stellarator configuration, using numerical calculations at a reference point. Examples for these calculations are inductances, peak field calculations or stellarator forces.

The fully three-dimensional shape of the coils is assumed to be fixed, but the sizes of the coils are scaled from the HELIAS 5-B values to the geometrical values for the machine being modelled using fundamental physics and engineering principles.

The stellarator coils are assumed to be superconducting - no resistive coil calculations are performed. The critical field at the superconductor is calculated using circular approximations for the coils in the inductance and field calculations, and the limit is enforced automatically. All superconductor materials that are available for tokamaks are also available for stellarators.

The winding pack cross-section is rectangular for the stellarator coils, rather than the two-step cross-section assumed for tokamaks. The coil thicknesses and most of the dimensions of the materials within the coil cross-section are outputs from the model, instead of being inputs as is the case for tokamaks; see the variable descriptor file for details. In addition, certain iteration variables (tfcth, no. 13; thkcas, no. 57; cpttf, no. 60 and tftort, no. 77) should not be turned on in the input file as they are calculated self-consistently (thkcas is required as input); the code will stop with an error message of this is attempted. The conduit insulation thickness (thicndut), as well as the steel thickness around each conductor (thwcndut) should be given as input parameters together with the dimension of the conductor area (t_turn_tf).

stellarator-PROCESS returns a set of parameters for the coil force densities, which are scaled from the reference calculation. The user should check if the value max_force_density, which gives the toroidally and radially averaged maximum value of the volumetric force density in MN/m$^3$ and needs to be held from the winding pack structural material is within reasonable regions and eventually adapt the winding pack composition. max_force_density_Mnm is the integrated force density in MN/m and should be bound by icc = 32.

A reasonable set of input parameters for the stellarator coil module is the following set:

i_tf_sc_mat = 8 * Switch for superconductor material in tf coils;
sig_tf_wp_max = 4.e8 * Maximal allowable Stress level on Ground insulation for a simple stellarator coil stress module (Pa)
fcutfsu = 0.7 *Copper fraction of cable conductor (TF coils), Schauer: 900 SCU strands, 522 Copper strands. Value for 0.4 Helium
tftmp = 4.75 *Peak helium coolant temperature in TF coils and PF coils (K)
tmpcry = 4.75 * Temperature in TF coils, required for plant efficiency (K)
vftf = 0.3 *Coolant fraction of TF coil leg (itfsup=0) this is the same for conductor and strand!
fiooic = 0.78 *Fraction TF coil critical current to operation current (should be iteration variable!)
vdalw = 12.64 * Max voltage across tf coil during quench (kV)
tdmptf = 20 * Dump time (should be iteration variable)
thkcas = 0.1 * Thickness TF Coil case (for stellarators: Also for toroidal direction)
t_turn_tf = 0.048 * Dimension conductor area including steel and insulation. Important parameter.
thicndut = 0.0015 * Conduit insulation thickness (one side) (m)
thwcndut = 0.006 * thickness of steel around each conductor (one side) (m)
tinstf = 0.1 * insulation on top of winding pack (one side) (m)

Machine build

Since a stellarator is inherently non-axisymmetric, the build of the PROCESS stellarator is defined at the most critical position in radial and toroidal direction. The radial and toroidal build consistency is enforced by the constraint equations 82 and 83.

The surface areas of for the first wall, blanket and shield components are scaled linearly with their effective minor radius from the plasma surface area calculation(the area of a simple torus of circular cross-section is $4\pi^2Ra$, hence the linear scaling with $a$). The input parameters fhole may be used to specify the hole fraction, to adjust the surface area to take into account of ports and divertors, for instance. The volume of the first wall etc. are simply given by the product of their surface area and their mean thickness.

In contrast to tokamaks, which in PROCESS are assumed to have a cylindrical external cryostat completely surrounding the fusion power core, the stellarator model assumes that the external cryostat (labelled as the outer vessel in Figure 1) is toroidal with a circular cross-section. Its cross-section is assumed to be centred at the mean plasma major radius.

All items external to the fusion power core (buildings, turbines, power conversion systems, etc.) remain unchanged.

Stellarator Blanket

There are two blanket modules implemented in stellarator-PROCESS at the moment, - blktmodel = 1: Calls the KIT HCPB model - blktmodel = 0 AND ipowerflow=1: Calls a "simple" model (ipowerflow=0 is even simpler and not advised)

The KIT HCPB model is documented elsewhere, for the simple module the following set of input parameters should be provided:

blkttype = 0,1,2 (only relevant for mass calculations)
emult = 1.18 *Energy multiplication in blanket and shield
etahtp = 1. *Electrical efficiency of primary coolant pumps
fblbe = 0.47 *Beryllium fraction of blanket by volume (only relevant for mass calculations)
fblli2o = 0.07 *Lithium oxide fraction of blanket by volume (only relevant for mass calculations)
fbllipb = 0. *Lithium lead fraction of blanket by volume (only relevant for mass calculations)
fblss = 0.13 *Stainless steel fraction of blanket by volume (only relevant for mass calculations)
fblvd = 0. *Vanadium fraction of blanket by volume (only relevant for mass calculations)
fhole = 0. *Area fraction taken up by other holes (in addition to fdiv and fhcd when ipowerflow=1)
fwclfr = 0.1 *First wall coolant fraction (only relevant for mass calculations)
primary_pumping = 1 *Switch for pumping power (0: User sets pump power directly)
htpmw_blkt = 120. *Blanket coolant mechanical pumping power (MW)
htpmw_fw = 56. *First wall coolant mechanical pumping power (MW)
htpmw_div = 24. *Divertor coolant mechanical pumping power (MW)
secondary_cycle = 2 *Switch for power conversion cycle (2: user input thermal-electric efficiency)
vfblkt = 0.1 *Coolant void fraction in blanket (blktmodel=0) (only relevant for mass calculations)
vfshld = 0.6 *Coolant void fraction in shield
declblkt = 0.075 *Neutron decay length in blanket area (m)
declfw = 0.075 *Neutron decay length in first wall (m)
declshld = 0.075 *Neutron decay length in shield area (m)
blnkith = 0.6 *Inboard blanket thickness (m)
blnkoth = 0.6 *Outboard blanket thickness (m)
ddwex = 0.15 *Cryostat thickness (m)
d_vv_in = 0.01 *Vacuum vessel thickness (TF coil / shield) (m)
gapds = 0.025 *Gap between inboard vacuum vessel and tf coil (m)
gapomin = 0.025 *Minimum gap between outboard vacuum vessel and TF coil (m)
scrapli = 0.15 *Gap between plasma and first wall; inboard side (m)
scraplo = 0.2 *Gap between plasma and first wall; outboard side (m)
shldith = 0.2 *Inboard shield thickness (m)
shldoth = 0.2 *Outboard shield thickness (m)
shldtth = 0.2 *Upper/lower shield thickness (m)
vgap = 0. *Vertical gap between x-point and divertor (m)

The simple stellarator blanket module is largely reduced to calculating masses given on blanket and shield sizes as defined in the input file. It also calculates neutron heat depositions based on the neutron decay length (this enters the cost function via shield pumping powers e.g.). Most of the blanket constraints implemented in tokamak PROCESS, namely icc=52,53,54,55 are not available with blktmodel = 0 and the KIT HCPB model, blktmodel = 1 should be used instead. Note, that PROCESS also features other blanket models (HCLL, WCLL) and thermohydraulic blanket models but they are not yet available for stellarators.

---

1. F. Schauer, K. Egorov and V. Bykov, "HELIAS 5-B magnet system structure and maintenance concept", Fusion Engineering and Design 88 (2013) 1619-1622 ↩↩↩

2. F. Warmer, "Stellarator Plasma Geometry model for the systems code PROCESS", IPP Greifswald, Germany, internal note, 19/06/2013 ↩

3. F. Warmer, "Stellarator Divertor model for the systems code PROCESS", IPP Greifswald, Germany, internal note, 21/06/2013 ↩↩

4. F. Warmer and F. Schauer, "Stellarator Coil model for the systems code PROCESS", IPP Greifswald, Germany, internal note, 07/10/2013 ↩

5. VMEC MHD force balance code for toroidal domains, http://vmecwiki.pppl.wikispaces.net/VMEC ↩↩

6. J. Lion et al, "A general Stellarator version of the systems code PROCESS", Nuclear Fusion, 61 (2021) 126021, doi.org/10.1088/1741-4326/ac2dbf. ↩↩↩↩

7. J. Nuhrenberg et al., PLasma Physics and Controlled Fusion, 35 (1993) B115 ↩

8. S. Sudo, Y. Takeiri, H. Zushi et al., Nuclear Fusion, 30 (1990) 11 ↩↩

9. R. J. Goldston, H. Biglari, G. W. Hammett et al., Bull. Am. Phys. Society, 34 (1989) 1964 ↩

10. K. Lackner and N. A. O. Gottardi, Nuclear Fusion, 30 (1990) 767 ↩

11. U. Stroth et al., Nuclear Fusion, 36 (1996) 1063 ↩

12. H. Yamada et al., Nuclear Fusion, 45 (2005) 1684 ↩

13. T. Andreeva et al., The Helias Reactor Concept: Comparative Analysis of Different Field Period Configurations, Fusion Science and Technology, 46 (2004) doi.org/10.13182/FST04-A579 ↩

14. C. Zhu et al. New method to design stellarator coils without the winding surface, Nucl. Fus. 58 (2018) 016008 doi.org/10.1088/1741-4326/aa8e0a ↩

15. J. Lion Systems Codes Models for stellarator fusion power plants and application to stellarator optimization, PhD Thesis (TU Berlin) (2022) to appear ↩