VMCON Optimisation Solver Explained

Introduction

To give the user a better understanding of the optimisation solver implemented in PROCESS and the interpretation of its results, we give a short introduction into the mathematical background for solving these type of problems as well as the specific algorithm.

In section 1 , the general nonlinear programming problem is defined, which is the mathematical description of our problem. This problem is typically formulated using Langrange multiplier (c.f. section 2) and is solved numerically most efficiently using sequential quadratic programming (c.f section 3). The fotran subroutine that is used to implement such an optimisation solver in PROCESS is called VMCON (c.f. section 4), which iterates between solving a local quadratic subproblem (c.f. section 5) and a one dimensional line search (section 6). As the method uses a quasi-Newtonian approach the Hessian matrix is approximated by a variant of the Broyden-Fletcher-Goldfarb-Shanno update (c.f. section 7). Section 8 summarises the symbol convention used in this chapter.

1 - The General Non Linear Programming Problem

Mathematically the general non-linear programming problem or non-linear constrained optimisation problem is defined as:

$$\begin{align} \label{eqn:equation-1a} \tag{1a} \mathrm{minimise \, } f(\vec{x})\\ \label{eqn:equation-1b} \tag{1b} \mathrm{subject \, to \, } c_i(\vec{x}) &= 0, & i&=1,\dots,k,\\ \label{eqn:equation-1c} \tag{1c} \mathrm{and \, } c_i(\vec{x}) &\geq 0, & i&=k+1,\dots,m, \end{align}$$

where both the objective function $f(\vec{x})$ and the constraints $c_i(\vec{x})$ are non-linear functions of the $n$-dimensional vector of variables $vec{x}$ with bounds $\vec{x} \in \Omega$. In this context, all $\vec{x} \in \Omega$ that fulfill the constraints $c_i(\vec{x})$ are called feasible. They describe the allowed space in which we are trying to optimise the objective function $f(\vec{x})$. Note that any maximisation problem can be written as a minimisation by using $f_{new}(\vec{x}) = - f(\vec{x})$ and that any equality constraint $c(\vec{x}) = a$ can be rewritten as $c_{new}(\vec{x}) = c(\vec{x}) - a = 0$. Any inequality constraint can therefore by rearranged analogously to fit the form described in eq. \ref{eqn:equation-1c}. Please note that what is called figure of merit in PROCESS is called object function in the mathematical optimisation context. Hence, both names are used equivalently in this document.

2 - The Lagrange Method

The general non-linear programming problem can be solved mathematically using Lagrange's method. It assumes that the constraints cannot be used to explicitly reduce the parameters space of the iteration variables - as it is typically the case for non-linear constraints and objective functions - and is therefore a powerful method applicable to a general class of problem.

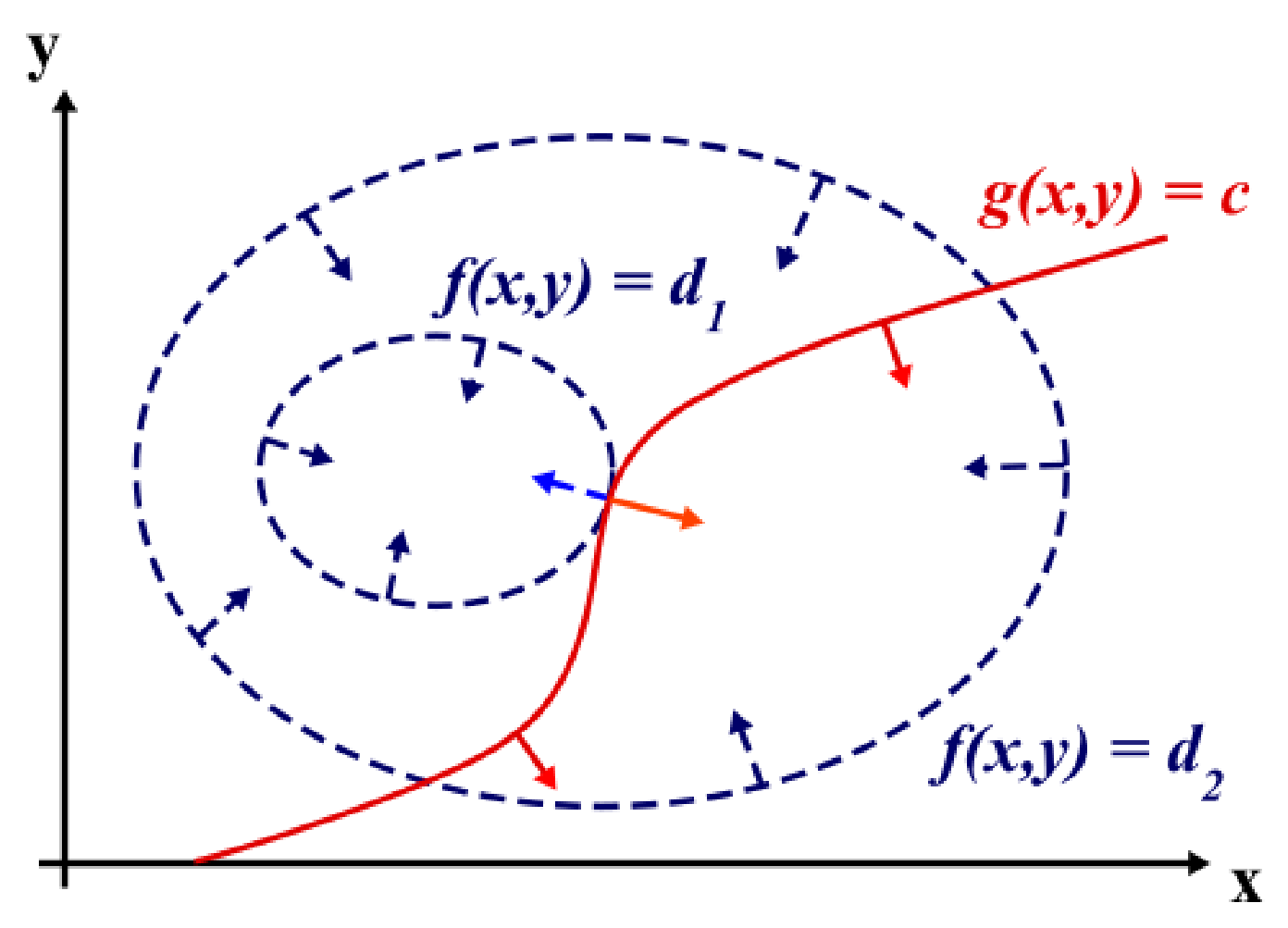
If we assume for simplicity that we have a 2D problem with only one equality constraint $c(x,y) = 0$, we know that we only need to search for the optimum along that constraint. At the optimum, the value of the objective function will then be stationary, i.e. it does not locally increase or decrease along the constraint. As the gradient of a function is perpendicular to its contour lines of $f(x,y) = d$, this is equivalent to saying that the gradient of the objective function at that point is parallel to the gradient of the constraints:

$$\begin{equation} \label{eqn:equation-2} \tag{2} \nabla f(x,y) = - \lambda \nabla c(x,y), \end{equation}$$

where the factor $\lambda$ is necessary as only the direction, but not the magnitude nor the sign of the gradients need to be equal. This is also illustrated in Figure 1.

Figure 1: Illustration of Lagrange Multiplier Method (credit Wikipedia) showing two contour lines of the objective function $f(x,y) = d_i$ (dark blue dashed lines) and the nonlinear constraint $g(x,y) = c$ (red solid line) as well as their gradients (blue and red arrows) at various positions including the constrained optimum (light blue and orange arrows).

When expanding the method to several equality and inequality constraints we can make use of the Lagrange function. For the non-linear programming problem described by The General Non-linear Programming Problem it is given by

$$\begin{equation} \label{eqn:equation-3} \tag{3} L(\vec{x},\vec{\lambda}) = f(\vec{x}) - \sum_{i=1}^{m} \lambda_i c_i(\vec{x}), \end{equation}$$

with the corresponding Lagrangian multipliers $\lambda_i$. It allows us to formulates the first order necessary conditions for a constrained optimum $\vec{x}^*$ with corresponding Lagrange multipliers $\vec{\lambda}^*$, the Karush-Kuhn-Tucker (KKT) conditions,

$$\begin{align} \label{eqn:equation-4a} \tag{4a} \nabla_x L(\vec{x}^*,\vec{\lambda}^*) &= \nabla_x f(\vec{x}^*) - \sum_{i=1}^{m} \lambda_i \nabla_x c_i(\vec{x}^*) = 0,&&\\ \label{eqn:equation-4b} \tag{4b} \lambda^*_i c_i(\vec{x}^*) &= 0, &i&=1,\dots,m,\\ \label{eqn:equation-4c} \tag{4c} c_i(\vec{x}^*) &= 0, &i&=1,\dots,k,\\ \label{eqn:equation-4d} \tag{4d} \lambda^*_i &\geq 0, &i&=k+1,\dots,m,\\ \label{eqn:equation-4e} \tag{4e} c_i(\vec{x}^*) &\geq 0, &i&=k+1,\dots,m. \end{align}$$

Please note that by construction the Lagrange multipliers $\lambda_i^*$ fulfilling the KKT conditions are describing the derivative of the objective function with respect to the constraint equations $\frac{df}{dc_i}$ and are therefore a measure of how much the objective function changes with respect of each constraint.

In the special case of a continually differentiable convex objective function $f(\vec{x})$ and equality constraints as well as affine inequality constraints, these KKT conditions are also sufficient for a global optimum. The PROCESS optimisation solver has been designed to converge on the KKT conditions, but does not test whether these are sufficient for a global optimum. It is therefore crucial that the user verifies that a global optimum has been found.

Furthermore, these conditions and therefore the solver, assume that both the objective function and constraints are at least first order continuously partially differential, i.e. that their first order partial derivatives are all continuous functions. This might not always be the case in PROCESS and is a potential source of errors.

3- Sequential Quadratic Programming (SQP)

Based on the Lagrange method, sequential (also successive or recursive) quadratic programming is the most efficient method to numerically solve constrained non-linear optimisation problems ¹. It combines a simple solver for a quadratic optimisation problem with linear constraints that determines a search direction $\vec{\delta}$ with a line search to find an optimum along that search direction. It is a type of the more feasible direction methods which is itself a type of primal method that solve non-linear programming problems in the $n - m$ dimension feasible subspace².

4- VMCON

The optimisation solver implemented in PROCESS is the Fortran routine VMCON³. It is a modified version of the vf02ad routine from the Harwell Software Library (www.hsl.rl.ac.uk) and implements a SQP method originally suggested by Powell⁵ (this should not be confused with Powell's algorithm⁴ which solves a multidimensional unconstrained minimisation problem without derivatives) based on work by Han⁶. As stated before VMCON is designed to converge on a solution of the necerssary KKT conditions (eq. \ref{eqn:equation-4e}), but does not check the sufficient conditions. Its convergence criterion is therefore given by

$$\begin{equation} \label{eqn:equation-5} \tag{5} \left| \nabla_x f(\vec{x}^{j-1})^T \cdot \vec{\delta}^{j} \right| + \sum^m_{i=1}\left| \lambda^j_i c_i(\vec{x}^{j-1}) \right| < \texttt{epsvmc} \end{equation}$$

where epsvmc is a user specific error tolerance, $\vec{\delta}^j$ is the vector in direction of the next line search (c.f. line search) and $j$ is the counter of the sequential quadratic programming iteration. Hence, the first part estimates the predicted improvement due to the next line search and the second part measures the error in the complimentary condition eq \ref{eqn:equation-4b} of the KKT conditions.

Figure 2 describes the flow chart of the VMCON routine, while the various values of the return parameter ifail (within the VMCON routine ifail is called info) are described and interpreted in Table 1.

Figure 2: This is the flow chart of the VMCON optimisation solver. The criteria for and the interpretation of the successful (ifail = 1) and unsuccessful (ifail $\neq$ = 1) return parameters are described in Table 1

ifail	Description	Meaning	Recommendation
0	VMCON: Improper input parameters	The input parameters to the solver are wrong, e.g. negative number of iteration variables.	This needs to be fixed on the developer side and should only occur in the test phase of the new modules.
1	VMCON: Normal return	VMCON has found a solution that fulfills the necessary conditions within the specified error tolerances (c.f eq. \ref{eqn:equation-5})	Test whether the solution is a global solution by using different starting parameters.
2	Too many function calls	During the line searchVMCON has reached the maximum number of total function calls (maxfev=100)	VMCON struggles to find a solution. Retry with different start parameters.
3	Line search required 10 function calls	The results produced by input objective function/constraints and their gradients are inconsistent. This can be due to numerical noise in the input functions.	The developer needs to check the consistency and numerical robustness of the objective function, constraints and their derivatives. Perhaps the accuracy in numerical integrations/differentiations needs to be higher. As a user, try changing the iteration bounds or adding other iteration variables.
4	Uphill search direction was calculated	The quadratic subproblem has suggested a search direction in which the objective function only increases.	This happens if an inconsistency between the objective function, the constraints and their respective derivatives occurs (c.f. ifail=3)
5	qpsub: no feasible solution or bad approximation of Hessian	Either no optimum lies within the space allowed by constraints and variable bounds or the identity matrix is not a good first approximation of the Hessian.	As a user, add a new iteration variable, as developer, try using a multiple of the identity matrix as initial Hessian instead.
6	qpsub: Singular matrix in quadratic subproblem or restriction by artificial bounds	This is fairly self-explanatory.	If this is meaningful, widen the boundaries of the iteration variables.

Table 1: Summary of the description and meaning of the VMCON return parameters ifail.

5 - The Quadratic Subproblem (QSP)

Within sequential quadratic programming the complex nonlinear problem is broken down into solving a sequence of local quadratic subproblems with linear constraints. This is based on the assumption that locally the problem is well approximated by a second order Taylor expansion of the Lagrange function. Hence, the local quadratic subproblem is described by

$$\begin{align} \label{eqn:equation-6a} \tag{6a} \mathrm{minimise} \,\, &Q(\vec{\delta}) = f(\vec{x}^{j-1}) + \vec{\delta}^T \nabla_x f(\vec{x}^{j-1})+ \frac{1}{2} \vec{\delta}^T \nabla_{xx} L(\vec{x}^{j-1},\vec{\lambda}^{j-1})\vec{\delta} \\ \label{eqn:equation-6b} \tag{6b} \mathrm{subject to} \,\, &\vec{\delta}^T \nabla_x c_i (\vec{x}^{j-1}) + c_i(\vec{x}^{j-1}) = 0,\ i = 1,\dots,k,\\ \label{eqn:equation-6c} \tag{6c} \mathrm{and} \,\, &\vec{\delta}^T \nabla_x c_i (\vec{x}^{j-1}) + c_i(\vec{x}^{j-1}) \geq 0,\ i = k+1,\dots,m, \end{align}$$

where $\vec{\delta} = \vec{x} - \vec{x}^{j-1}$, the index $j-1$ indicates the parameter values of the previous iterations ($j$ is called nqp in the VMCON routine) and $\nabla_{xx}L(\vec{x}^{j-1},\vec{\lambda}^{j-1})$ is the Hessian of the Lagrange function. The solution of the QSP $\delta$ describes the change of the current iteration variable vector that minimises the local approximation of the problem. To assure convergence even from bad starting points, it is not directly used to update the iteration variable vector, but describes the direction of the line search in which a 1d function is minimised using a Newtonian method (c.f. Line Search). Being a second order approximation to the original problem, it typically has a faster convergence that sequential linear programming (SLP) methods [⁷, chap. 10.4].

To allow the applicability of the solver to more general problems, Powell⁵ substituted the Hessian $\nabla_{xx}L(\vec{x}^{j-1},\vec{\lambda}^{j-1})$ with a positive definite approximation B. This mean that both the objective function $f(\vec{x})$ and the constraint equations $c_i(\vec{x})$ only have to be continuously differentiable instead of twice continuously differentiable with respect to the iteration variable vector $\vec{x}$. This makes the method a Quasi-Newtonian method as opposed to a true Newtonian method. How this approximation is initialised and updated is described in more detail in the section about the Broyden-Fletcher-Goldfarb-Shanno update (BFGS).

To solve the QSP VMCON uses harwqp a modification of the Harwell library routine VE02AD, which in itself uses the subroutine harwfp/LA02AD to find a feasible point within the variable bounds and linearised constraints. Both routines go back to a method by Fletcher^{8 9 10}. The Lagrange multipliers are also determined from results of the harwqp routine.

If the routine cannot fund a feasible point it fails with ifail = 5 (c.f. Table 1). As the routine is only checking the local linear approximation of the constraints rather than the full non-linear constraints, there is a chance that a feasible point exists even though the routine fails with ifail = 5. In these cases, it is possible that the first approximation of the Hessian has not been good and the algorithm has, therefore, taken an inappropriately large step. Then using a multiple of the identity matrix will convergence of the algorithm.

If a singular matrix is encountered with the QSP solver or the solution is restricted by the artificial bounds, VMCON fails with ifail = 6. In this case it can be helpful to widen the boundaries of the iteration variable.

6 - The Line Search

The line search is an essential part of the SQP algorithm. As Powell⁵ pointed out, it is necessary to allow convergence from poor starting conditions. It uses the vector $\vec{\delta}$ from the QSP to update $\vec{x}^j = \vec{x}^{j-1} + \alpha^j \vec{\delta}^j$ where the step-length parameter $\alpha^j > 0$ is determined by the line search as the parameter that minimises

$$\begin{equation} \label{eqn:equation-7} \tag{7} \Phi(\alpha) = f(\vec{x}) + \sum_{i=1}^k \mu_i \left| c_i(\vec{x})\right| + \sum_{i=k+1}^m \mu_i \left| min(0,c_i(\vec{x}))\right| \end{equation}$$

where the weights are defined as

$$\begin{equation} \mu_i = \begin{cases} \label{eqn:equation-8} \tag{8} |\lambda_i^1| & \mathrm{if} \quad j = 1,\\ max\left(|\lambda_i^j|,1/2(\mu_i^{j-1} + |\lambda_i^j|)\right) & \mathrm{if} \quad j > 1 \end{cases} \end{equation}$$

to assure maximally efficient convergence⁶. Note, that in this method locally inactive inequality constraints are not having any effect. It should always be possible, to find a solution that fulfills

$$\begin{equation} \label{eqn:equation-9} \tag{9} \Phi(\alpha=0)> \Phi(\alpha^j), \end{equation}$$

if

$$\begin{equation} \label{eqn:equation-10} \tag{10} \left. \frac{d \Phi}{d\alpha}\right|_{\alpha=0} < 0. \end{equation}$$

In case the derivative is positive (dflsa $\geq$ 0), an uphill search direction has been determined and the code stops with ifail = 4. This typically only happens, if the objective function or constraints are inconsistent with their own derivatives.

As the line search tries to determine the optimum of a one dimensional, but fully non-linear function $\Phi(\alpha)$, it creates a series of $\alpha_l$ values (In the actual code $\alpha =$ calpha and $\alpha_l =$ alpha $*\alpha_{l-1}$). At each iteration $l$, a quadratic local function $\Phi_l(\alpha)$ fulfilling the boundary conditions $\Phi_l(0) = \Phi(0)$, $\Phi'_l(0) = \Delta$ and $\Phi_l(\alpha_{l-1}) = \Phi(\alpha_{l-1})$ is minimised, where typically $\Delta = \Phi'(0)$. This leads to

$$\begin{equation} \label{eqn:equation-11} \tag{11} \Phi_l(\alpha) = \Phi(0) + \Delta \alpha + \frac{\Phi(\alpha_{l-1})-\Phi(0) - \Delta \alpha_{l-1}}{\alpha_{l-1}^2} \alpha^2 \end{equation}$$

and minimising this gives

$$\begin{equation} \label{eqn:equation-12} \tag{12} \alpha_{min} = - \frac{\Delta\alpha_{l-1}^2}{2(\Phi(\alpha_{l-1})-\Phi(0) - \Delta \alpha_{l-1})}. \end{equation}$$

Powell then sets $\alpha_l = \min(\alpha_{min}, 0.1\alpha_{l-1})$. On each iteration the convergence of the line search is tested. It is reached, if

$$\begin{equation} \label{eqn:equation-13} \tag{13} \Phi(\alpha_l) - \Phi(0) < 0.1 \Delta. \end{equation}$$

which assures that the change in the function is small in comparison to its derivative and 0.1 is a factor determined by experience. If this criterion is successful, the code exits the line search and updates all function evaluations.

As a modification to the original code, we have added an adhoc fix that exits the line search in the case of

$$\begin{equation} \label{eqn:equation-14} \tag{14} \Phi(\alpha_l) - \Phi(0) > 0. \end{equation}$$

This has been added as experience have shown that VMCON typically does not converge in these situations, but if it is forced to calculate a new search direction in this way, it sometimes successfully finishes. Note, that this cannot force VMCON to converge on any false solutions, as it only exits positively when the convergence criterion (eqn \ref{eqn:equation-5}) is fulfilled.

Typically, the line search already converges after one iteration and, therefore, $\alpha = 1$. Hence, the VMCON line search has an upper limit of maximally 10 iterations before it terminates with ifail = 3 (c.f. table 1). This is higher than Powell's original limit of 5 to avoid a few cases of early termination without a major effect on efficiency.

Within the line search VMCON also checks that the total number of function calls has not exceeded maxfev = 100. If this is the case, it exits with error code ifail = 2. Both checks assure that the routine stops, if it does not seem to be able to fund a solution.

7 - The Broyden-Fletcher-Goldfarb-Shanno (BFGS) quasi-Newton update

VMCON uses a quasi-Newtonian update, the Broyden-fletcher-Goldfarb-Shanno update, in the approximation of the Hessian of the Lagrange function. This means it is applicable to all continuously differentiable objective and constraint functions. Note, that due to the constraints it is not actually necessary for the Hessian of the solution to be positive definite, even though this is essential for the convergence of the algorithm.

In quasi-newtonian methods the identity matrix I is often chosen as an initial estimate of the Hessian because of its positive definiteness. In some cases it can be helpful to chose a constant multiple of the identity of the identity matrix instead. The BGFS update¹¹ is one way of revising the initial Hessian approximation using the update of the iteration variable vector

$$\begin{equation} \label{eqn:equation-15} \tag{15} \vec{\xi} = \vec{x}^{j} - \vec{x}^{j-1} \end{equation}$$

and the update of the Jacobian of the Lagrange function

$$\begin{equation} \label{eqn:equation-16} \tag{16} \vec{\gamma} = \nabla_x L(\vec{x}^j,\vec{\lambda}^{j}) - \nabla_x L(\vec{x}^{j-1},\vec{\lambda}^{j}). %NOT \lambda^{j-1}!!! \end{equation}$$

Note that unless $\alpha = 1$ in the line search, $\vec{\xi} \neq \vec{\delta}$. To assure the positive definiteness of B Powell⁵ suggested a variation of the standard formalism that uses $\vec{\eta}$ instead of $\vec{\gamma}$

$$\begin{equation} \label{eqn:equation-17} \tag{17} \vec{\eta} = \theta \vec{\gamma} + (1-\theta) \mathbf{B} \vec{\xi} \end{equation}$$

with

$$\begin{equation} \label{eqn:equation-18} \tag{18} \theta = \left\{ \begin{array}{lr} 1 & \vec{\xi}^T \vec{\gamma} \geq 0.2 \vec{\xi}^T \mathbf{B} \vec{\xi} \\ \frac{0.8 \vec{\xi}^T B \vec{\xi}}{\vec{\xi}^T} & \vec{\xi}^T \vec{\gamma} < 0.2 \vec{\xi}^T \mathbf{B} \vec{\xi} \end{array} \right. \end{equation}$$

to calculate a new approximation to the Hessian

$$\begin{equation} \label{eqn:equation-19} \tag{19} \mathbf{B}_{new} = \mathbf{B} - \frac{\mathbf{B} \vec{\xi} \vec{\xi}^T \mathbf{B}}{\vec{\xi}^T \mathbf{B} \vec{\xi}}+\frac{\vec{\eta}^T \vec{\eta}}{\vec{\xi}^T \vec{\eta}}. \end{equation}$$

Using the modified version of the BFGS update as suggested by Powell, furthermore, assures superlinear convergence, even if the true Hessian is indefinite¹².

8 - Symbols

In the previous sections the following conventions have been assumed: $\vec{x}$, $\vec{\delta}$, $\vec{\xi}$, $\vec{\gamma}$ and $\vec{\eta}$ are $n$-dimensional vectors, where $n$ is the number of iteration variables. $\vec{c}$, $\vec{\lambda}$, $\vec{\mu}$ are $m$-dimensional vectors, where $m$ is the total number of constraints and $c_i, \lambda_i$ and $\mu_i$ ($i=1\dots m$) are their respective components. $\mathbf{B}$ and $\mathbf{I}$ are $n\times n$-dimensional matrices, while $\nabla_x \vec{c}$ is an $n\times m$-dimensional matrix.

References

---

1. P.J. Knight. Nonlinear Programming Codes. Springer, Berlin, 1980. ↩

2. D. G. Luenberger and Yinyu Ye. "Linear and Nonlinear Programming". International Series in Operations Research and Management Science. Springer Science and Business Media LCC,, 3^rd edition edition, 2008. ↩

3. R.L. Crane, K.E. Hillstrom, and M. Minko. Solution of the general nonlinear programming problem with subroutine vmcon. Argonne National Laboratory Report ANL-80-64, 1980. ↩

4. M.J.D. Powell. An efficient method for finding the minimum of a function of several variables without calculating derivatives. Computer Journal, 1964. ↩

5. M.J.D. Powell. A fast algorithm for nonlinearly constrained optimization calculations. Lecture Notes in Mathematics, Springer-Verlag, Berlin, 630:144{157, 1978. ↩↩↩↩

6. S.-P. Han. A globally convergent method for nonlinear programming. Technical Report 75-257, Department for Computer Science, Cornell University, 1975. ↩↩

7. H. D. Sherali M. S. Bazaraa and C. M. Shetty. "Nonlinear Programming: Theory and Algorithms". John Wiley & Sons, Inc., New York, 1993. ↩

8. R. Fletcher. A general quadratic programming algorithm. Technical Report T.P. 401, Atomic Energy Research Establishment, 1970. ↩

9. R. Fletcher. The calculation of feasible points for linearly constrained optimisation problems. Technical Report R.6354, Atomic Energy Research Establishment, 1970. ↩

10. R. Fletcher. A fortran subroutine for general quadratic programming. Technical Report R.6370, Atomic Energy Research Establishment, 1970. ↩

11. M. Avriel. Nonlinear programming: Analysis and methods. Dover Publications, Inc., Mineola, NY, 2003. ↩

12. M.J.D. Powell. The convergence of variable metric methods for non-linearly constrained optimisation calculations. presented at Nonlinear Programming Symposium 3, Madison, Wisconsin, 1977. ↩